ublo
bogdan's (micro)blog

bogdan » ideas for the modern computer

08:12 am on Oct 1, 2012 | read the article | tags: nice2know

modern computer has its roots in scientific computing service ltd, a british company incorporated by leslie comrie in 1937. the company owned thousand of parallel computers scatter across the country, the “processors” being women working in teams and performing steps from complex algorithms, helped by rudimentary mechanical calculators. this model served as inspiration for alan turing‘s ideas.

reference: nature 486, 12 june 2012, pg. 321
photo source: bbc history

bogdan » modern spies don’t use microphones

10:44 pm on Sep 28, 2012 | read the article | tags: nice2know

an article for all my paranoid friends and acquaintances.

i love spy movies. i really do. with little to no exception most of them depict the use of “bugs” to spy on a conversation. more, due to our communist legacy, we (romanians) are proficient at spying. romanian “bugs” were generously (re)covered by our media: here, here and here. unfortunately most of these stories are focused on pretty old, flawed technology.

the “bug”, no matter how small and miniaturized, has a built in weakness: it has to send the information collected to the listener and the preferred medium is modulating an electromagnetic field and actively transport it. needless to say that power sources are involved requiring maintenance.

a better, safer and passive way of spying on other people should start from the definition of a microphone:

microphone: an instrument capable of transforming sound waves into changes in electric currents or voltage, used in recording or transmitting sound.

first, capturing sound is quite easy: the pressure waves travel through an elastic medium bouncing of various surfaces, including windows. the glass is a relatively elastic medium and forced by the sound waves inside – vibrates, transporting inside information to the outside world.

but is there a device capable of measuring the tiny vibration of windows, from a relatively safe distance, in order to recover the leaked information? of course, and it’s around from 1897 when michelson and morley laid the foundation of special theory of relativity: the michelson-morley interferometer. a tool used to measure tiny length variations made by current technologies cheap and suited for spying.

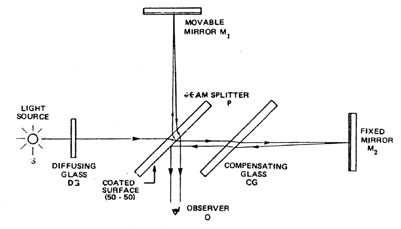
the above picture shows a sketch of the apparatus. any vibration of the movable mirror M1 – actually the spied window – is translated in a variation of the interference pattern, simple enough to be analyzed in real time and converted into sound. using infrared laser diodes (extremely cheap and easy to process with a webcam) you get an invisible, passive, hard to detect “bug”. there are some technical difficulties but any student with basic understanding of the interference process is able to solve them.

my security advice: along with searching for hidden microphones one should be careful talking in a room with outside windows. and no, thermopane® windows are not immune but a thick curtain can greatly improve your privacy.

photo source: here.

bogdan » viteza sunetului în vid (sic)

08:26 am on Sep 17, 2012 | read the article | tags: nice2know

mi-am adus aminte de o afirmație prezentată ca «Fact» în numărul din august al «Știință și Tehnică»:

Viteza sunetului în vid este de aproximativ 1100 km/h.
(S&T / august 2012 / pg. 12)

chiar și cea mai atehnică persoană, cu acces la DEX și noțiuni elementare de logică își poate da seama de inepția unei astfel de afirmații:

SÚNET, sunete, s. n. 1. Vibrație a particulelor unui mediu elastic care poate fi înregistrată de ureche.
VID, -Ă, vizi, vide, adj., s. n. 1. Adj. (Despre un spațiu) Care nu conține nimic; care nu conține aer sau alt gaz; care nu este ocupat, locuit; pustiu.
(DEX’98)

altfel spus, în vid, unde nu există particule care să vibreze, sunetul nu se poate transmite. în articol apare totuși o valoare, 1110 km/h. fiind legat de saltul cu parașuta a lui Felix Baumgartner, de la 29455m, pot să vă spun cu certitudine că viteza respectivă se referă la viteza sunetului la altitudinea de la care s-a realizat saltul, unde încă mai există atmosferă și mediu elastic prin care să se propage unda sonoră.
valoarea corectă variază în funcție de temperatură, între 1062 Km/h (-57°C) și 1083 Km/h (-48°C).

pentru pasionații de calcule, puteți încerca să determinați viteza sunetului folosind formula următoare:
$$v = \sqrt {\gamma \frac {p}{\rho}}$$
unde γ = indexul adiabatic,
p = presiunea atmosferică,
ρ = densitatea aerului;
sursă foto: Smith College

bogdan » 1st incompletness theorem

12:35 am on Sep 15, 2012 | read the article | tags: nice2know

or better stated, unless we have infinite uncountable processing power we will never be able to describe the universe starting from our knowledge.

in 1931, at 25 years old, Kurt Goedel proved two theorems central to modern science. named incompleteness theorems, they set a bound on the limit of our knowledge at a specific time, pushing the “know it all” objective far beyond any imaginable horizon and extending our quest indefinitely.

1st incompletness theorem (as stated by Stephen Cole Kleene in 1967)

Any effectively generated theory capable of expressing elementary arithmetic cannot be both consistent and complete. In particular, for any consistent, effectively generated formal theory that proves certain basic arithmetic truths, there is an arithmetical statement that is true, but not provable in the theory.

in simple words the theorem states that starting with a finite set of rules that can generate numbers and simple arithmetic on them, there are statements that cannot be proven or unproven using only the starting rules. more over, there’s no algorithm that can extend (even infinitely) the initial set of rules in order to cover all the statements involving the constructed numbers. the theorem scales up to the size of the universe as all modern physics theories extend the simple arithmetic on natural numbers, thus in any physical system (as understood today) there are properties of the system components that will lay outside the boundaries of our knowledge.

definitions: uncountably infinite.

photo: Oskar Morgenstern, institute of advanced study archives

bogdan » surreal numbers

09:15 pm on Sep 10, 2012 | read the article | tags: nice2know

the field of surreal numbers is the largest totally ordered field that can be constructed. it’s nice2know because of the elegant construction and the neat ideas behind it.

let’s start with a totally ordered set and a rule:

“given two subsets, L and R of the initial set, with L strictly less than R, {L|R} will denote the number strictly greater than L and strictly less than R”.

we can now elegantly construct:

{|} ~ 0 (where both L and R are empty sets);
{0|} ~ 1 (where L={|} and R is empty);
{1|} ~ 2 … {n|} ~ n+1, thus embedding the natural numbers.

making L empty and R one of the “naturals” we get negative integers: {|n} ~ -n-1

we can extend further the initial set closing it with respect to {0|1} ~ 1/2 and thus embedding the dyadic numbers set, which is a dense set in reals.

following the density of dyadic numbers, for any real number a we can construct infinite dyadic subsets L and R for which L < a < R, i.e. {L|R} ~ a.

the construction goes even further, building transfinite numbers like {{1,2,3,…}|} ~ ω and {0|{1/2,1/4,1/8,…}} ~ ε.

warning:
each surreal number has more than one representation, much like fractions. ex: 1/2 ~ {0|1} ~ {1/4|3/4}. this is why i avoided to use {0|} = 1.

definitions:
field, totally ordered set, dense set, transfinite number

painting: joan miro – dancer