ublo
bogdan's (micro)blog

bogdan » how to build a maze

01:42 pm on Oct 7, 2018 | read the article | tags: howto

in this post i’ll use C to construct a maze, that will be later used for my swarm experiments.

i’ll be using a graph-model for the maze: each vertex is a room from the maze, which is connected by edges to other rooms. in a 2-D classic maze of size m×n, with m spanning from top to bottom and n spanning from left to right, each room has at most 4 neighbors. this means each vertex in my graph will have at most 4 edges: top, bottom, left and right. the total number of edges is m&times(n-1) for vertical edges (top, bottom) and (m-1)×n for horizontal edges (left, right). in order to create a maze, in the previously described graph, i’ll choose using a version of Dijkstra algorithm a maximum spanning tree. to make the maze random, i’ll mark each edge with a random weight and then run the maximum spanning tree algorithm.

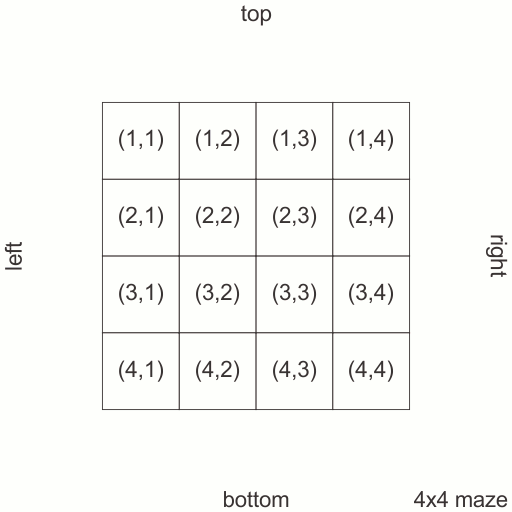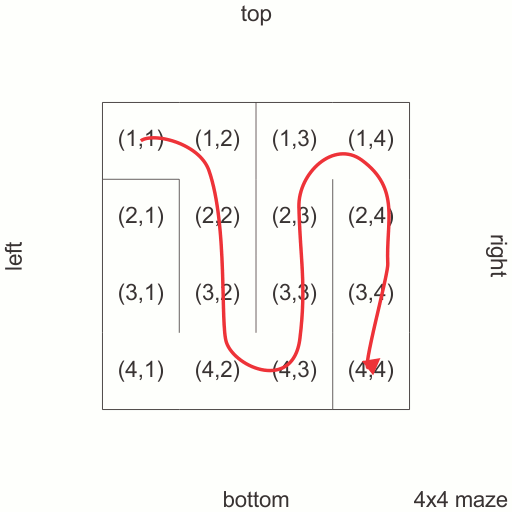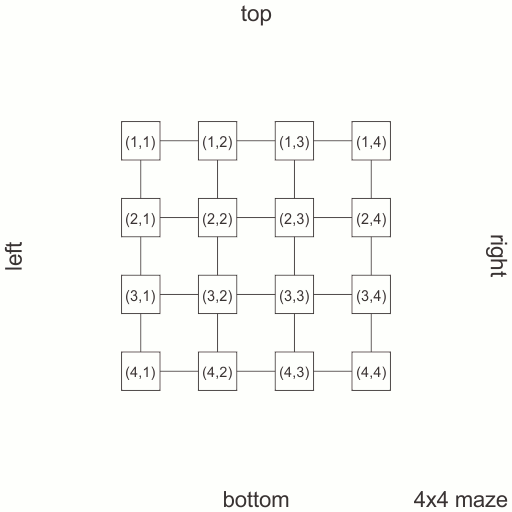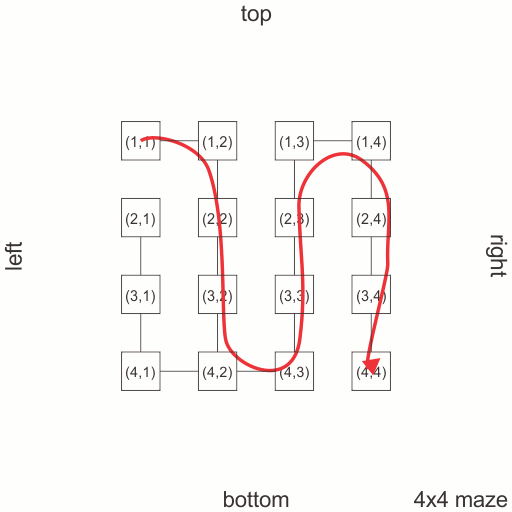
i’ll be using matrices as data structures. this means that each vertex will be labeled with a pair (i,j) with i from 0 to m-1 and j from 0 to n-1. as the graph is not oriented, i’ll have:

• if (i,j) is linked to (i,j+1), than i’ll store in my matrix, on position (i,j) the weight of the edge [(i,j),(i,j+1)];
• if (i,j) is linked to (i+1,j), than i’ll store in my matrix, on position (i,j+n) the weight of the edge [(i,j),(i+1,j)];
• no need to store the [(i,j),(i,j-1)] edge as it’s equivalent to [(i,(j-1)),(i,(j-1)+1)];
• also, no need to store connections at the lower and right edge of the maze;

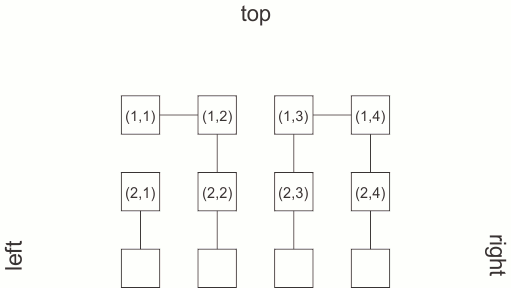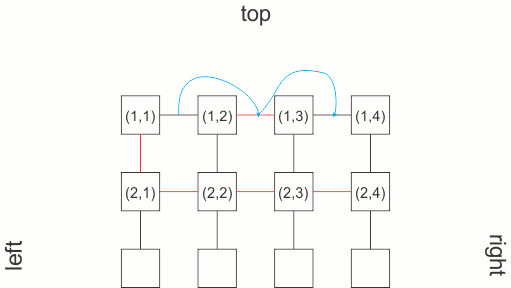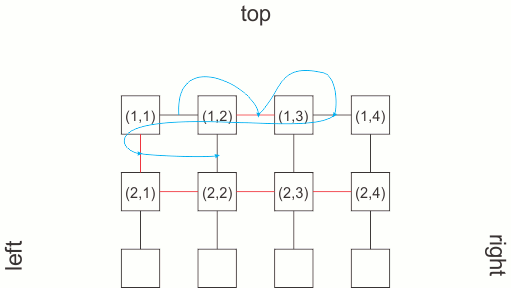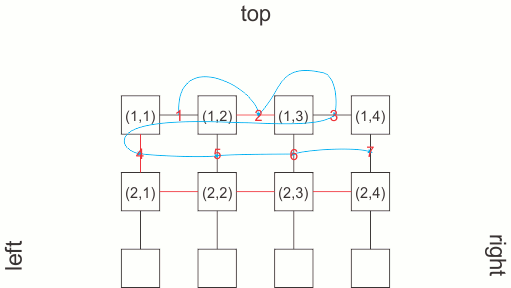
the number of required edges’ weights can be held in a m×(2×n-1)-n vector, corresponding to an incomplete m×(2×n-1) matrix.

building the weight matrix

this step is quite easy. just loop over all m×(2×n-1)-n and assign them a random value between 1 and 255. i’ll be using 0 to represent edges that are missing.

/**
 * the function initializes the weights matrix as described above;
 * @param m (int) the dimension of the maze on top-bottom axis;
 * @param n (int) the dimension of the maze on left-right axis;
 * @returns: an uint8_t matrix, of size (m-1)*2*(n-1) filled with random data;
 */
uint8_t * maze_weight_init (int m, int n) {
        /** @var maze the weight matrix */
        uint8_t * maze;
        /** @var c is  a variable index */
        int c;

        /** i reserve the space in the computer memory for the matrix */
        maze = (uint8_t *) malloc ((m * (2 * n - 1) - n) * sizeof (uint8_t));
        /** if memory reservation is successful, i'm filling the matrix */
        if (maze != NULL)
                for (c = 0; c < m * (2 * n - 1) - n; c++)
                        *(maze + c) = (uint8_t) ((1 + rand ()) % 256);

        return maze;
}

tip:
the matrix is stored as a single vector, meaning a cell on the position (i,j) can be accessed by finding as the (i×cols+j)-th component of the vector. this map is bijective, meaning that the i-th component of the vector corresponds to position (i/cols, i%cols) in the matrix, where / is the integer division and % is the reminder operator.

sorting the weight matrix

the matrix is not useful like this. it needs to be sorted. i'm using a simple (inefficient) bubble sort algorithm. i'll take advantage of how i stored the matrix so i can simply arrange the associated vector. i'll create a vector into which i'll keep the association of indices.

bubble sort works like this: take the first weight from the vector, and if it's heavier that the one above, swap their places. this has to be repeated until the entire vector is sorted: this happens when there are no swaps on a swipe.

/** the function is sorting the associated vector V, returning a mapping of the
 * sorted indices, M, with V(i) being the original vector, while V(M(i)) is the sorted one
 * @param weights (uint8_t *) is the original vector
 * @param m (int) is the top-bottom size of the maze
 * @param n (int) is the left-right size of the maze
 * @returns: an int mapping vector between the sorted version and the original one
 */
int * maze_edges_sort (uint8_t * weights, int m, int n) {
        /** @var indices the vector containing the sorted mapping */
        int * indices;
        /**
         * @var c a variable index
         * @var t a temporary variable used in swapping two indices
         * @var o a temporary variable storing last index swapped
         * @var l, initially the length of the weights vector,
         *        after, the length of the unsorted vector
         */
        int c, t, o, l = m * (2 * n - 1) - n;

        /** initialize indices with an identity mapping i->i */
        indices = (int *) malloc (l * sizeof (int *));
        for (c = 0; c < l; c++)
                *(indices + c) = c;

        if (indices != NULL)
                /** while there's still some unsorted part of the vector */
                while (l > 0) {
                        /** o holds the last swapped value */
                        o = 0;
                        /** i'm looping until the end of the unsorted vector */
                        for (c = 1; c < l; c++) {
                                /** if the weights don't respect the sort order, swap them */
                                if (*(weights + *(indices + c - 1)) > *(weights + *(indices + c))) {
                                        /**
                                         * of course, i'm swapping indices in the mapping,
                                         * not real values, as the initial vector remains
                                         * unchanged, only the mapping function deviates from
                                         * identity map
                                         */
                                        t = *(indices + c - 1);
                                        *(indices + c - 1) = *(indices + c);
                                        *(indices + c) = t;
                                        /** store the last swapped index */
                                        o = c;
                                }
                        }
                        /** the length of the unsorted vector equals the last swapped index */
                        l = o;
                }

        return indices;
}

building the maximum spanning tree

this algorithm is more complex that the previous ones. for easier understanding, i need to explain some notions:

• a graph is a collection of vertices and edges, each edge connecting two vertices; it can and usually has loops - meaning starting from one vertex, it can be reached again going edge-by-edge; like a city with ring-roads;
• a tree is a graph with no loops; it means that starting with a vertex, and going edge-by-edge you'll never get to the same vertex again; like a computer network;
• in a graph (including a tree), a sub-tree is a collection of vertices and edges from the initial graph that behave like a tree - there are no loops;

i'll start with an empty set of sub-trees from the original graph. this will be called a forest set. forests have at least one tree. at the end of the algorithm i'll have in this set a tree that will link all vertices from the original graph. this is called a maximum spanning tree.

with each sorted edge, lighter to heavier, i'll do the following:

• if the edge is not connected to any sub-tree from my sub-tree set, i'll add the edge to the sub-tree set, coloring it with a new color;
• if the edge has one vertex connected to a sub-tree in my sub-tree set, i'll add the edge to the sub-tree set, coloring it with the same color as the rest of the sub-tree;
• if the edge has vertices on different sub-trees, than i'll add the edge and color both sub-trees, as well as the edge, with a common color. i'll use indexed colors, so i'll choose the minimum color;
• if the edge has vertices on the same sub-tree, i'll skip this edge; in this situation, the edge is creating a loop in the tree, making it a graph;

/**
 * the procedure takes as parameters a weight matrix together with its size
 * and modifies in place the weights matrix, removing the unnecessary edges
 * an edge is kept, if the weight is strict positive, while an edge is
 * deleted, if its weight is zero.
 * @param weights (uint8_t *) is the weight vector
 * @param m (int) is the maze top-bottom size
 * @param n (int) is the maze left-right size
 */
void maze_init (uint8_t * weights, int m, int n) {
        /**
         * @var indices is the sorted mapping for the weights vector;
         * @var matrix is a vector-stored matrix that has 0 on (i,j)
         *         0 on (i,j) position, if the (i,j) vertex was not visited
         *         color>0 on (i,j) position, if the (i,j) vertex was visited
         *         and (i,j) is part of the "color" sub-tree
         */
        int * indices, * matrix;
        /**
         * @var c,d are variable indices;
         * @var row,col are the row and column indices in the @see matrix
         * @var n_row,n_col are the indices for the vertex connected to
         *        (row,col);
         * @var min_color is the minimum "color" when merging an existing
         *        sub-tree with a new edge. the edge can link two existing
         *        sub-trees, meaning i'll have to choose a single color for both
         * @var max_color is analog with @see min_color;
         * @var color is the current available color for new sub-trees;
         */
        int c, d, row, col, n_row, n_col, min_color, max_color, color = 1;

        /** reserve memory for the is-visited? matrix */
        matrix = (int *) malloc (m * n * sizeof (int));
        for (c = 0; c < m * n; c++)
                *(matrix + c) = 0;

        /** sort the graph weights */
        indices = maze_edges_sort (weights, m, n);

        /** loop through sorted edges */
        for (c = 0; c < m * (2 * n - 1) - n; c++) {
                /** get the edge first vertex label as (row, col) */
                row = *(indices + c) / (2 * n - 1);
                col = *(indices + c) % (2 * n - 1);

                /**
                 * based on how is stored, get the label for the
                 * second vertex associated with the edge
                 */
                if (col < n - 1) {
                        n_row = row;
                        n_col = col + 1;
                }
                else {
                        col = col - n + 1;
                        n_row = row + 1;
                        n_col = col;
                }

                /**
                 * check if the current edge can be added to the forest:
                 * the edge needs to fulfill all requirements:
                 * - the edge is not already part of a tree, meaning that both
                 *        vertices are the same non-zero color
                 */
                if (
                        (*(matrix + row * n + col) == *(matrix + n_row * n + n_col)) &&
                        *(matrix + row * n + col) > 0
                ) {
                        *(weights + *(indices + c)) = 0;
                        continue;
                }

                /**
                 * find the color of the new vertices, by getting minimum and
                 * maximum color. both can be zero, if we start a new sub-tree
                 */
                if (*(matrix + row * n + col) < *(matrix + n_row * n + n_col)) {
                        min_color = *(matrix + row * n + col);
                        max_color = *(matrix + n_row * n + n_col);
                }
                else {
                        min_color = *(matrix + n_row * n + n_col);
                        max_color = *(matrix + row * n + col);
                }

                if (min_color == 0) {
                        /**
                         * here, min = max = 0, this means we have a new sub-tree
                         * so i color it with the next available color
                         */
                        if (max_color == 0) {
                                *(matrix + row * n + col) =
                                *(matrix + n_row * n + n_col) = color ++;
                        }
                        /** here, the edge has an open end, the other is connected */
                        else {
                                *(matrix + row * n + col) =
                                *(matrix + n_row * n + n_col) = max_color;
                        }
                }
                else {
                        /**
                         * here min, max > 0, both different, this means that the
                         * edge is connecting two different color sub-trees, so i
                         * make both the same color (min color)
                         */
                        *(matrix + row * n + col) =
                        *(matrix + n_row * n + n_col) = min_color;

                        for (d = 0; d < m * n; d++)
                                if (*(matrix + d) == max_color)
                                        *(matrix + d) = min_color;
                }
        }

        /** remember to free the reserved memory */
        free (indices);
        free (matrix);
}

putting it all together

piece of cake. first, i'll have to initialize my weights. than, to build the maximum spanning tree. a good exercise is to display the maze on the screen using ASCII art.

#include  /** required for malloc, srand and rand functions */
#include  /** useful for printing stuff, with printf */
#include  /** i need the uint8_t definition */
#include  /** i need the time function */

/**
 * this is the normal, unix-style format for the program entrypoint
 * @param argc (int) is the number of arguments from the command line;
 * @param argv (char **) is an array of strings, containing the command line arguments;
 * @returns: an integer, zero if no error has occurred.
 */
int main (int argc, char ** argv) {
        /** @var weights (uint8_t *) my weights matrix */
        uint8_t * weights;
        /** @var m, n (int) the maze size */
        int m = 4, n = 4;

        /** make the random numbers random :-) */
        srand (time (NULL));

        /** initialize the weights matrix */
        weights = maze_weight_init (m, n);
        /** build a maximum spanning tree from the matrix */
        maze_init (weights, m, n);

        /** tell the operating system that there's no error */
        return 0;
}